# Decision Tree
- 분류와 회귀 작업, 다중 출력 작업 가능
- 매우 복잡한 데이터셋 학습 가능
- 랜덤 포레스트(Random Forest) 의 기본 구성 요소
# 학습과 시각화
사이킷런의 DecisionTreeClassifier 모듈을 통해 결정 트리 모델 학습 가능, Graphviz 를 통해 결정 트리 시각화 가능
예시) iris 데이터셋의 꽃잎 길이와 꽃잎 너비 데이터를 이용하여 클래스 분류하기
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
export_graphviz() 함수를 사용하여 그래프 정의를 .dot 파일로 출력, 훈련된 결정 트리 시각화
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file=image_path("iris_tree.dot"),
feature_names=["꽃잎 길이 (cm)", "꽃잎 너비 (cm)"],
class_names=iris.target_names,
rounded=True,
filled=True
)
import graphviz
with open("images/decision_trees/iris_tree.dot") as f:
dot_graph = f.read()
dot = graphviz.Source(dot_graph)
dot.format = 'png'
dot.render(filename='iris_tree', directory='images/decision_trees', cleanup=True)
dot
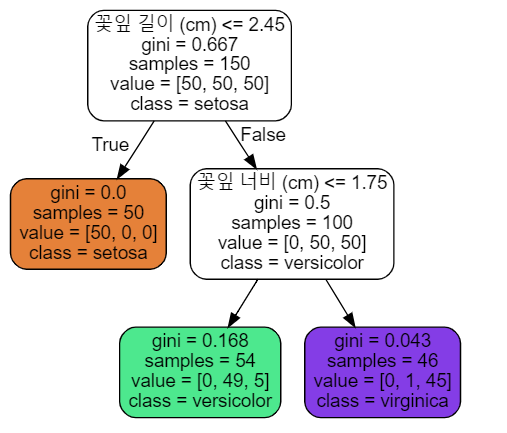
위 그림에서 노드마다 gini, samples, value, class 변수가 있는 것을 볼 수 있음
samples : 얼마나 많은 훈련 샘플이 적용되었는지
gini : 불순도 (해당 노드의 클래스가 아닌 샘플이 차지하는 비중)
value : 각 클래스에 얼마나 많은 훈련 샘플이 있는지
#예측
- 루트 노드(root node, 가장 맨 위의 노드)에서 시작
- 새로운 샘플을 노드의 조건에 검사 -> 위 그림에선 True 일 경우, False 일 경우 해당 자식 노드로 이동
- 리프 노드(leaf node, 자식 노드가 더 이상 없는 노드) 일 경우 해당 노드의 클래스로 예측
$i$ 번째 노드의 gini 불순도
$$G_i = 1 - \sum_{k=1}^{n} p_{i,k}^2 $$
$p_{i,k}$ : $i$ 번째 노드 훈련 샘플 중 클래스 $k$ 에 속한 비율
장점: 데이터 전처리가 거의 필요하지 않음

위 그림은 훈련시킨 결정 트리의 결정 경계를 나타낸 것
굵은 수직선 : 루트 노드의 결정 경계 (depth = 0)
위의 그림은 깊이가 2인 결정 트리에 의한 결정 경계
하이퍼파라미터 max_depth를 통해 결정 트리의 깊이를 지정할 수 있음
# 클래스 확률 추정
어떤 샘플 $mathrm{x}$ 가 주어지면 샘플에 대한 리프 노드를 탐색
해당 노드에 있는 클래스 $k$ 의 훈련 샘플 비율 반환
if) 해당 노드의 value 가 [0 , 45 , 5] 이면 [0.0 , 0.9 , 0.1] 을 반환 --> 클래스 1 을 출력
CART 알고리즘
먼저 훈련 세트를 하나의 특성 $k$ 의 임곗값 $t_k$ 를 사용해 두 개의 서브셋으로 나눔
$k$ 와 $t_k$ 를 고르는 기준은 다음의 비용함수를 최소화하는 $(k, t_k)$ 를 찾는 것
CART 비용 함수
$$ J(k,t_k) = \frac{m_{\text{left}}}{m} G_{\text{left}} + \frac{m_{\text{right}}}{m} G_{\text{right}} $$
$G_{\text{left/right}}$ 은 왼쪽/오른쪽 서브셋의 불순도
$m_{\text{left/right}}$ 은 왼쪽/오른쪽 서브셋의 샘플 수
훈련 세트를 성공적으로 분할하면 분할된 서브셋을 같은 방식으로 나누는 과정 반복.
max_depth 로 정의된 최대 깊이가 되거나 불순도를 줄이는 분할을 찾을 수 없을 때 중지
* CART 알고리즘은 탐욕적 알고리즘이며 최적의 솔루션은 보장하지 않음( 최적 트리를 찾는 문제는 $\mathrm{NP}$-$\mathrm{Complete}$ 문제, 시간 복잡도 $O(e^m)$ 그러므로 납득할 만한 좋은 솔루션으로 만족해야 함
# 계산 복잡도
균형 잡힌 이진 트리일 경우 일반적인 결정 트리 탐색 계산 복잡도는 $O(log_2 m)$
훈련 알고리즘은 각 노드에서 모든 훈련 샘플 $m$ 의 모든 특성 $n$ 을 비교하므로
계산 복잡도는 $O(n\times m log m)$
# 엔트로피 불순도
사이킷런에서 criterion 매개변수를 "entropy" 로 지정하여 엔트로피 불순도를 사용할 수 있음
엔트로피 불순도
$$H_i = - \sum{k=1}^{n} p_{i,k} log_2 (p_{i,k}) ,\quad p_{i,k} \neq 0 $$
지니 불순도 VS 엔트로피 불순도
- 실제로 큰 차이는 없음
- 지니 불순도가 조금 더 계산 빠름 -> 일반적으로 사용
- 지니 불순도는 불순도가 가장 빈도 높은 클래스를 한쪽 가지로 고립
- 엔트로피 불순도는 비교적 더 균형 잡힌 트리 만듦
# 회귀
각 노드에서 클래스를 예측하는 대신 어떤 값을 예측

회귀에서는 불순도 대신 MSE 를 최소화하도록 분할함.
회귀에서의 비용함수
$$J(k, t_k) = \frac{m_{\text{left}}}{m} MSE_{\text{left}} + \frac{m_{\text{right}}}{m} MSE_{\text{right}} $$
$$MSE_{\text{node}} = \sum_{i \in \text{node}} (\hat{y}_{\text{node}} - y_i)^2$$
$$\hat{y}_{\text{node}} = \frac{1}{m_{\text{node}}} \sum_{i \in \text{node}} y_i $$
회귀 작업에서도 결정 트리가 과대적합되기 쉬움.
min_samples_leaf 등 규제 파라미터를 증가시켜 모델을 규제할 수 있음 (리프 노드당 최소 샘플 개수)
(max 로 시작하는 파라미터는 감소시킬수록 모델이 규제됨)
# 불안정성
제한사항: 결정 트리는 계단 모양의 결정 경계를 만들어서 훈련 세트의 회전에 민감함
-> PCA 기법: 훈련 세트를 더 좋은 방향으로 회전
또한 훈련 데이터의 작은 변화에 아주 민감하며 예측이 확률적임(예를 들어 특성 개수를 데이터셋보다 작게 설정하면 무작위적으로 일부 특성이 선택됨)
=> 랜텀 포레스트 : 많은 트리에서 만든 예측을 평균하여 결정, 불안정성을 극복
이미지 출저: handson-ML translator github
'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| [Keras Deep Learning] 신경망 Tutorial (0) | 2020.04.18 |
|---|---|
| 핸즈온 머신러닝(8) - 앙상블 학습 (2) | 2020.01.29 |
| 핸즈온 머신러닝(6) - 서포트 벡터 머신 2 (0) | 2020.01.27 |
| 핸즈온 머신러닝(6) - 서포트 벡터 머신 1 (1) | 2020.01.27 |
| 핸즈온 머신러닝(5) - 로지스틱 회귀 2 (0) | 2020.01.24 |




댓글