핸즈온 머신러닝(3) - 머신러닝 프로젝트 3

# 데이터 이해를 위한 탐색과 시각화

 -이번 프로젝트에서는 훈련 세트에 대해서만 탐색, 훈련 세트가 매우 클 경우 탐색을 위한 세트를 별도로 샘플링 할 수도 있다. 예제에 나온 훈련 세트는 크기가 작으므로 훈련 세트 전체를 사용함.

 

 - 먼저 훈련세트의 손상 방지를 위해 복사본을 만들어두도록 한다.

housing = strat_train_set.copy()

-지리 정보(위도, 경도)가 있으므로 모든 구역을 산점도로 만들어 데이터를 시각화해 본다.

ax = housing.plot(kind="scatter", x="longitude", y="latitude")
ax.set(xlabel='longitude', ylabel='latitude')

지리적인 산점도

 - 위 산점도만 보아서는 특별한 패턴을 딱히 찾을 수 없어 보인다. alpha 옵션을 0.1로 줘서 데이터 포인트가 밀집된 영역을 살펴본다.

ax = housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
ax.set(xlabel='경도', ylabel='위도')

alpha = 0.1을 적용한 결과

- 무언가 보이는 듯 하다. 밀집된 지역은 점이 짙게 표시된 것을 볼 수 있다. 

 

이제 아래의 코드를 이용하여 주택 가격을 나타내 본다. 매개변수 s 에 해당하는 원의 반지름은 구역의 인구(population)을 나타내며 색깔은 가격(매개변수 c)을 나타낸다. 사전 정의된 컬러 맵 중 파란색(낮은 수치)~빨간색(높은 수치)까지의 범위를 가지는 jet 을 사용한다(매개변수 cmap).

ax = housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
    s=housing["population"]/100, label="population", figsize=(10,7),
    c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
    sharex=False)
ax.set(xlabel='longitude', ylabel='latitude')
plt.legend()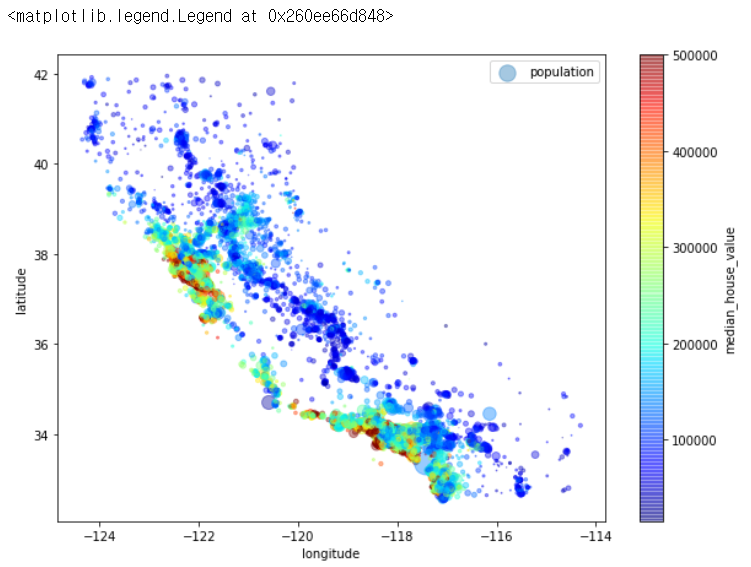

원의 반지름은 구역의 인구, 원의 색깔은 주택의 평균 가격을 나타낸다.

 - 위에 나온 두 개의 그래프를 보면, 첫번째 그래프의 인구밀도가 높은(점이 짙은) 지역과 두번째 그래프의 주택 가격이 높은(점의 색이 빨간색에 가까운) 지역이 어느정도 일치하는 것을 볼 수 있다. 또한 그 지역들은 바다와 인접해있다는 공통점도 알 수가 있다. (이런 내용은 군집 알고리즘을 사용해 주요 군집을 찾고 군집의 중심까지의 거리를 재는 특성을 추가할 때 도움이 된다.)

 

 

# 상관관계 조사

 - 데이터셋이 아주 크지 않으므로 모든 특성 간의 표준 상관계수(standard correlation coefficient)를 corr() 메서드를 이용하여 쉽게 계산할 수 있다.

corr_matrix = housing.corr()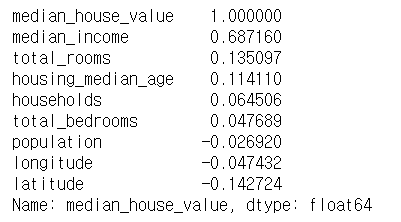

corr_matrix["median_house_value"].sort_values(ascending=False)   의 결과

 - 상관관계의 범위는 -1~1까지이며, 1에 가까울수록 양의 상관관계를 나타낸다. 위 수치를 보면 중간 소득은 중간 주택 가격과 어느정도 비례하는 관계를 가진다는 것을 볼 수 있다. 계수가 0에 가까우면 선형적인 상관관계가 없다는 뜻이다.

 

- pandas의 scatter_matrix 함수를 이용해서도 특성 사이의 상관관계를 확인할 수 있다. scatter_matrix 함수는 숫자형 특성 사이에 산점도를 그려준다. 아래 코드는 몇 개의 특성만을 뽑아 그 상관관계를 도출한 것이다.

from pandas.plotting import scatter_matrix

attributes = ["median_house_value", "median_income", "total_rooms",
              "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))

 * scatter_matrix 메서드의 diagonal 매개변수로 히스토그램을 나타내는 'hist'와 커널 밀도 추정을 나타내는 'kde'를 지정할 수 있다. 기본값은 'hist'이다.

산점도 행렬. median_income 과 median_house_value가 상관관계가 있는 것으로 나타난다.

 - 중간 주택 가격(median_house_value)와 중간 소득(median_income)으로 상관관계 산점도를 확대해보면

housing.plot(kind="scatter", x="median_income", y="median_house_value",
             alpha=0.1)
plt.axis([0, 16, 0, 550000])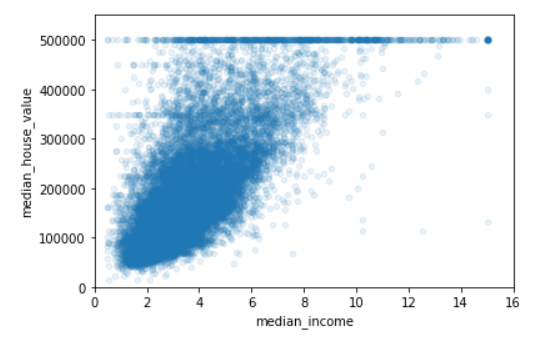

중간 소득과 중간 주택 가격의 상관관계를 나타내는 plt그래프

 - 상관관계가 아주 강하게 나타난다. 양의 상관관계를 보이며 포인트들이 충분히 밀집되어 있다. 또한 가격 상한선 값이 500,000$ 이기 때문에 수평선으로 나타난다. 그러나 그 밑의 가격구간, 450,000$ 근처, 350,000$ 과 280,000$ 에도 수평선이 보이며 그 아래도 조금 보인다. 이때는 알고리즘이 이런 이상한 형태를 학습하지 않도록 해당 구역을 제거하는 것이 좋다.

 

# 특성 조합으로 실험

 - 머신러닝 알고리즘용 데이터를 실제로 준비하기 전에 마지막으로, 여러 특성의 조합을 시도해볼 수 있다. 예를 들어 우리가 가진 데이터의 'total_rooms' 항목과 'households' 항목을 조합하여 '가구당 방의 개수' 라는 데이터를 만들어 낼 수 있다. 

housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]

데이터들을 조합하여 가구당 방의 개수, 방 당 침대 개수, 가구당 인구 수 라는 데이터를 만들어냈다.

이들을 이용하여 상관관계 행렬을 확인해본다.

새로 만들어진 bedrooms_per_room은 total_bedrooms 보다 중간 주택 가격과 상관관계가 높은 것을 볼 수 있다.